Matamos ou não matamos?

Agora eu me pergunto, “matamos” ou não “matamos” a matemática? Neste trimestre, acho que ainda não deveria ser feita a execução desta. Gostei um pouco dessa matéria, espero no próximo trimestre não mudar de ideia.

Comentários;

É, digamos que está matéria não é assim TÃO difícil. Claro, demorei um pouquinho para me organizar, mas acho que entendi bem. Algumas partes da matéria talvez sejam desnecessárias, assim como outras precisamos mesmo. É engraçado saber que tudo tem um tamanho exato e que podemos saber este tamanho depois de algumas contas “simples”.

Tetraedro (Geometria Espacial);

O tetraedro regular é um sólido platônico representante do elemento fogo.
Possui 4 vértices , 4 faces e 6 arestas. Considerado como um caso particular de pirâmide regular de base triangular, o volume do tetraedro regular é dado pela expressão matemática:

Pirâmides (Geometria Espacial);

Principais pirâmides: • Pirâmide Quadrada - aquela em que na base tem um quadrado.
• Pirâmide Triangular - aquela em que na base tem um triângulo.
• Pirâmide Pentagonal - aquela em que na base tem um pentágono.
• Pirâmide Quadrangular - aquela em que na base tem um quadrilátero.
Elementos:
• Base: A base da pirâmide é a região plana poligonal sobre a qual se apoia a pirâmide.

• Vértice: O vértice da pirâmide é o ponto isolado P mais distante da base da pirâmide.
• Eixo: Quando a base possui um ponto central, isto é, quando a região poligonal é simétrica ou regular, o eixo da pirâmide é a reta que passa pelo vértice e pelo centro da base.
• Altura: Distância do vértice da pirâmide ao plano da base.
• Faces laterais: São regiões planas triangulares que passam pelo vértice da pirâmide e por dois vértices consecutivos da base.
• Arestas Laterais: São segmentos que têm um extremo no vértice da pirâmide e outro extremo num vértice do polígono situado no plano da base.
• Apótema: É a altura de cada face lateral.
• Superfície Lateral: É a superfície poliédrica formada por todas as faces laterais.
• Aresta da base: É qualquer um dos lados do polígono da base.

Prismas (Geometria Espacial);

Prismas são sólidos geométricos que possuem as seguintes características:



• Bases paralelas são iguais;
• Arestas laterais iguais e paralelas e que ligam as duas bases.



Os prismas são nomeados pelo número de lados das bases:

 
 
 
 
 
 
 
 
 



Para calcular a área da superfície de um prisma, calcularemos a área das bases e a área das laterais (para calcular a área das laterais, calcularemos a área de todos os polígonos laterais e somaremos a área de todos eles), e somaremos a duas, formando a área total (At). Já para calcular o volume, usaremos a seguinte fórmula V = Bh, em que B é a área da base e h é a altura do prisma, que corresponde a aresta lateral do prisma.

Geometria Espacial;

É o estudo da geometria no espaço, onde estudamos as figuras que possuem mais de duas dimensões, essas figuras recebem o nome de sólidos geométricos ou figuras geométricas espaciais.
Visão espacial: Permite a percepção de formas espaciais, sem estar vendo fisicamente os objetos.

Círculo (Geometria Plana);

A área do círculo é igual a ¶ (constante com um valor de 3,14159...) multiplicado pelo quadrado do raio (R):

Hexágono (Geometria Plana);

É formado por 6 triângulos equiláteros e sua área pode ser obtida atráves da fórmula básica de área de triângulos

Losango (Geometria Plana);

A área dos losangos, em que d1é a diagonal maior e d2é a diagonal menor, é igual à metade do produto dessas diagonais:

Retângulo (Geometria Plana);

Da mesma forma que para os paralelogramos, a área de um retângulo é igual ao produto de sua base por sua altura:

Paralelogramo (Geometria Plana);

A área dos paralelogramos é igual ao produto de sua base por sua altura:

Trapézio (Geometria Plana);

Um trapézio tem por dimensões b1 de base maior, b2 de base menor e h de altura.



Para calcular sua área, temos:

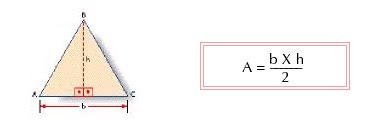
Triângulo (Geometria Plana);

A área de um triângulo é igual à metade do produto do comprimento de qualquer lado (base) pelo comprimento da altura correspondente:

Triângulo Equilátero:

É um caso especial de Triâgulo, isósceles, que apresenta não somente dois, mas todos os três lados iguais.

Área:

Altura:

Geometria Plana;

Estuda os espaços dimensionais, ou as superfícies das figuras geométricas. O conceito geral para o cálculo da área de uma superfície plana é: base X altura.

Os primeiros dias...

Nos primeiros dias de aula, tive alguns problemas de saúde e não compareci! Então, perdi todo o inicio da matéria. Quando voltei, recuperei o máximo que deu e acho que consegui...

Ciência dos números

Antes mesmo que consigamos matá-la, ela já nos matou. Ela vem matando milhões de pessoas a cada dia que passa.


Os cúmplices:
- Aritmética
- Álgebra
- Geometria
- Geometria Analítica
- Porcentagem
- Trigonometria
- Estatística
- Educação Matemática

2+2=4

Hoje eu acordei e advinha a primeira idéia que tive? Sim, exatamente essa: O que fazer no meu portfólio de matemática? Então consegui chegar a conclusão de que iria fazer um blog e ver no que ia dar. Aí vai...

(Portfólio para Professor Paulo; turma 301)

Nathália.